1° "F" TT

PROF.: ANA GRACIELA ALONSO. MATERIA: CIENCIAS SOCIALES

Los alumnos/as de 1º F trabajarán con la plataforma CLASSROOM como se había charlado en clase.
Les recuerdo el código de acceso para los que todavía no han ingresado; 6zg5nov
Buen comienzo!!!


-------------------------------------------------------------------------------------------------------------------

Ciencias Naturales- Profesora Mónica Marchese- 

Trabajo Práctico N° 1 " VIRUS"

1- ¿Cuáles son las características generales de los seres vivos?

2-¿ Cómo es un virus? Busca un esquema simple( dibujo, señalando y explicando sus partes)

3- Los virus....¿son considerados seres vivos? si-no ¿por qué?

4-¿Cómo ingresan los virus a nuestro organismo?

5- Nombra y explica brevemente,3 enfermedades causadas por virus( es muy importante , que al completar esta pregunta, busques en el diccionario las palabras que no comprendas). Explica los síntomas y tratamiento para cada una de ellas.


--------------------------------------------------------------------------------------------------------------------

EES N°  2

MATEMÁTICA

MEDINA VANINA

1°F

PROBLEMA 1

Lisandro tiene un camión y hace entregas de bebidas por todo el norte y el oeste del país. El lunes tiene que llevar diferentes cargas desde Buenos Aires hasta Mendoza, Tucumán, Salta y Jujuy. Para ahorrar combustible, debe decidir entre los siguientes recorridos:

a)       Buenos Aires –  Jujuy - Salta – Tucumán – Mendoza – Buenos Aires

b)       Buenos Aires -  Tucumán – Salta – Jujuy

En este cuadro, se muestran LAS DISTANCIAS EN Kilómetros entre ciudades:

                                Buenos Aires            Tucumán            Mendoza            Salta                  Jujuy

Buenos Aires            ---------                       1171                  1095                  1423                 1627

Tucumán                  1171                           -------                  980                    252                   275

Mendoza                 1095                            980                    --------                1232                 1255

Salta                         1423                            252                    1232                 -------                  113

Jujuy                         1627                           275                    1255                    113                  -------

¿Cuál será el recorrido más corto entre los dos que pensó, y cuántos kilómetros se ahorra?

PROBLEMA 2

Yamila le prestó a Pablo $275, y Pablo le prestó a Yamila $456. Marcar con una cruz el cálculo que permite conocer quién le debe a quién y cuánto le debe para saldar las deudas. Después resuélvelo

257 + 456                  275 – 456        456 – 275               456 x 275

PROBLEMA 3

Completar los datos que faltan en esta tabla de puntajes de un juego

Jugador                                   Primer ronda                           Segunda ronda           Tercer ronda                Total

Fernando                             15.469                                      7.250                            6.999                          ……………

Andrea                                 14.101                                      ……………………              9.265                          29.601                      

Adrián                                  …………………                            8.470                             9.500                          28.142

--------------------------------------------------------------------------------------------------------------------------
MATERIA   CONSTRUCION DE LA CIUDADANIA I
PROF. NORA SALIAS 
CURSOS  1°  F    y     1° E
Hola chicos!!  Espero que se encuentren bien , vamos a comenzar con algunas taréas

1. Elige de las siguientes opciones la que a tu criterio se acerca con el concepto de ciudadano y explica el por qué de la elección.

·                     Ir a la Iglesia

·                     Tener DNI

·                     Pagar los impuestos

·                     Ir al cine

·                     Hacer la cama

·                     Hacer la cola del supermercado

·                     Comprar un videojuego

·                     Votar a gobernantes

·                     Respetar el semáforo

·                     Cuidar el medio ambiente

2. Ubicar en una tabla las opciones del punto anterior entre DERECHOS y DEBERES u OBLIGACIONES.

--------------------------------------------------------------------------------------------------------------------------------------------

ED. ARTÍSTICA- PLÁSTICA 1° F

HOLA CHICOS SOY LA PROFESORA DE ARTISTICA  PLASTICA DE (1° F). ESTAS SON LAS ACTIVIDADES .

CONTINUIDAD PEDAGOGICA:       EDUCACION   ARTISTICA  

  PROFESORA: ROSA BEATRIZ  GIMENEZ                      CURSO  (1°F)             

OBJETIVOS GENERALES:    FAVORECER EL DESARROLLO DE LA PERCEPCION, EXPRESION Y COMUNICACIÓN. INTERPRETAR  LOS MENSAJES VISUALES.

EXPECTATIVAS DE  LOGROS: SELECCIONAR  ESTRATEGIAS, PARA LLEVAR A CABO SUS PROYECTOS, EXPRESIVOS Y COMUNICATIVOS.

CONTENIDOS: ELEMENTOS   PLASTICOS DEL LENGUAJE VISUAL    (LINEAS, COLOR, FORMAS, TEXTURA, IMAGEN POR COMPUTADORA, ETC).

ACTIVIDADES:

1) INVESTIGAR SOBRE ARTE EN LA PREHISTORIA:”ARTE PALEOLITICO Y NEOLITICO. BUSCAR SOBRE PINTURA, ESCULTURA, ARQUITECTURA Y CERAMICA. PEGAR ALGUNAS  IMÁGENES, O ILUSTRAR. 

2) INVESTIGAR: ¿QUE ES EL PUNTO?  ¿QUE  ES LA LINEA?  ¿QUE  TIPOS DE LINEAS HAY?

3) RECORTAR  VARIOS CUADRADOS Y CIRCULOS DE DIFERENTES TAMAÑOS, CON HOJAS DE COLORES O PAPEL GLASE. Y CREAR UNA COMPOSICION, ABSTRACTA O FIGURATIVA.

4) ELEGIR  UNA OBRA DEL PINTOR ARGENTINO   “QUINQUELA MARTIN “Y REALIZARLA, EN UNA HOJA  N° 6 Y PINTAR CON TEMPERAS.

16/3/20

FECHA DE ENTREGA   31 DE MARZO DEL 2020

---------------------------------------------------------------------------------------------------------------------------------

INGLÉS.

PROF. MARTA RANGO

Trabajaremos a través de classroom.

Código de la clase:  egsdia2

Los espero allí.

-----------------------------------------------------------------------------------------------------------------------------

Buenos días soy la profesora Marchese M de Ciencias Naturales nos vamos a comunicar por este medio y por classroom código n°obmomrn. Las actividades deben ser presentadas cuando se reinicien las clases
---------------------------------------------------------------------------------------------------------------------------------

NUMEROS NATURALES: primer parte

CONTENIDOS:

ü  MULTIPLICACIÓN

ü  DIVISIÓN

PROPIEDAD DISTRIBUTIVA

·        Copiamos los siguientes conceptos en la carpeta

Comencemos con la definición de números naturales

NÚMEROS NATURALES 

Se usan para contar y se los puede representar en una recta numérica, haciendo corresponder a cada número un punto. Se considerará que el 0 es un número natural. 

Los números naturales se simbolizan con la letra N.

Ø  Multiplicación y división. Propiedad distributiva

Los números que intervienen en una multiplicación y en la división tienen nombres especiales.

Aclaración: 7 x 9  = 7 . 9 , es decir el signo x  (POR) lo vamos a reemplazar por . (punto)

Multiplicación

                                                                a . b = c                                c es el producto

                                                                              a y b son factores

Por ejemplo

7 . 9 = 63  En éste ejemplo los factores serían el 7 y el 9 y el producto (resultado de la multiplicación) es el 63 

En la división tenemos al dividendo (D), resto (R), divisor (d), cociente (c). 

Por ejemplo             48      12

                                    0       4             

                                           

D= 48 es el dividendo

r=0 es el resto

d=12 es el divisor

c=4 es el cociente

48= 12 . 4 + 0

Ø  Propiedad distributiva de la multiplicación y de la división

Propiedad distributiva de la MULTIPLICACIÓN

Ingresemos al siguiente link  : https://www.youtube.com/watch?v=XIQOQrKP3uQ

Luego de mirar el video copiamos los siguientes ejemplos

	Sin aplicar propiedad distributiva (resolvemos primero el paréntesis)	Aplicando la propiedad distributiva
7 . ( 12 – 8 ) =	Resolvemos primero el paréntesis 7 . 4 =   28	Distribuimos el 7 hacia a derecha como lo muestran las flechas   7 . ( 12 – 8 ) = 7 . 12  - 7 . 8 = distribuimos el 7    84   -   56 = resolvemos la multiplicación          28
2 . ( 10 + 11 )	Resolvemos primero el paréntesis 2 . 21 = resolvemos el paréntesis   42      resolvemos la multiplicación	Distribuimos el 2 hacia a derecha como lo muestran las flechas 2 . ( 10 + 11 ) = 2 . 10  +  2 . 11 = distribuimos el 7    20   +   22 = resolvemos la multiplicación          42
Al resolverlo de dos formas distintas, vemos que da el mismo resultado (28 en el primer ejemplo y 42  en el segundo), entonces podemos afirmar que la multiplicación es distributiva respecto de la resta o de la suma a DERECHA  (distribuimos el 7 y el 2  hacia la derecha)

  

	Sin aplicar propiedad distributiva (resolvemos primero el paréntesis)	Aplicando la propiedad distributiva
(100 + 20 ) . 3	Resolvemos primero el paréntesis 120 . 3  =   360	Distribuimos el 3 hacia la izquierda como lo muestran las flechas   (100 + 20 ) . 3 = 100 . 3 + 20 . 3 = distribuimos el 3 300      +    60    = resolvemos la multiplicación       360 =              resolvemos la suma
(250 -  25 ) . 4	Resolvemos primero el paréntesis 225 . 4  =   900	Distribuimos el 4 hacia la izquierda como lo muestran las flechas (250 - 25 ) . 4 = 250 . 4 - 25 . 4 = distribuimos el 4 1000     -   100    = resolvemos la multiplicación       900                 resolvemos la suma
Al resolverlo de dos formas distintas, vemos que da el mismo resultado (360 en el primer ejemplo y 900  en el segundo), entonces podemos afirmar que la multiplicación es distributiva respecto de la resta o de la suma a IZQUIERDA  (distribuimos el 3 y el 4  hacia la IZQUIERDA)

Propiedad distributiva de la DIVISIÓN

Ingresemos al siguiente link  : https://www.youtube.com/watch?v=9qME7VbBgxc

Luego de mirar el video copiamos los siguientes ejemplos

	Sin aplicar propiedad distributiva (resolvemos primero el paréntesis)	Aplicando la propiedad distributiva
(30 + 12 ) : 6	Resolvemos primero el paréntesis 42 :  6  =   7           resolvemos la división	Distribuimos el 6 hacia la izquierda como lo muestran las flechas   (30 + 12 ) : 6 = 30 : 6 + 12 :  6 = distribuimos el 6 5     +    2    = resolvemos la DIVISIÓN       7 =              resolvemos la suma
Al resolverlo de dos formas distintas, vemos que da el mismo resultado (7 ) entonces podemos afirmar que la DIVISIÓN  es distributiva respecto de la resta o de la suma a IZQUIERDA  (distribuimos el 6 hacia la izquierda)

	Sin aplicar propiedad distributiva (resolvemos primero el paréntesis)	Aplicando la propiedad distributiva
200 :  ( 10 - 5 )	Resolvemos primero el paréntesis 200: 5 = resolvemos el paréntesis   40      resolvemos la multiplicación	Distribuimos el 2 hacia a derecha como lo muestran las flechas 200 : ( 10 - 5 ) = 200 : 10  -  200 : 5 = distribuimos el 200    20   -   40 = resolvemos la multiplicación          -20  da negativo
Al resolverlo de dos formas distintas, vemos que el resultado es DISTINTO (sin aplicar la propiedad distributiva da 40 y aplicando la propiedad distributiva da negativo 60), en conclusión la DIVISIÓN  NO ES DISTRIBUTIVA  respecto de la resta o de la suma a DERECHA  .

CONCLUSIONES:

ü La multiplicación es distributiva respecto de la suma y de la resta a derecha y a izquierda

La división es distributiva respecto de la suma y la resta SÓLO A IZQUIERDA

OBSERVACIÓN: indicamos que es distributiva, cuando al resolver de dos formas distinta un ejercicio (aplicando la propiedad y sin aplicar la propiedad) el resultado es el MISMO

                                                                  ACTIVIDADES

Actividad 1

Expresen las siguientes sumas como multiplicación, si es posible, y resuelvan

 a) 8+8+8+8+ = __________=_____

b)5 + 5 + 5        =__________=_____

c) 10 +10  = _____________=_____

d) 4+7 =________________= _____

 e) 7 + 6 + 16   = _________=______

 f) 14  + 14 + 14 + 14 =__________=_______

Ejemplo para resolver la actividad 1:

6 + 6 + 6 + 6 + 6 =   5 . 6 =  30

                                                                                      5 veces el 6

 Actividad 2

Resuelvan de dos maneras diferentes, cuando sea posible

	Aplicando la propiedad distributiva	Sin aplicar la propiedad distributiva
(95 + 25 ) : 5
5 . (15 – 8 )
520 : (5 + 8 )
13 . ( 7 + 9 )
(88 + 64 + 48 ) : 8
(33 + 17 – 5 ) . 4

 -----------------------------------------------------------------------------------------------------------------
 Chicos Educación Física 1ero F ,mi nombre es Gerardo Bonfanti, y a partir de hoy...los trabajos van a estar publicados en classroom donde semanalmente publicare los mismos el codigo del mismo es  7vwnumz y los trabajos seran entregados a mi mail. gerardobonfanti@gmail.com. cualquier duda sera a traves del classrom saludos.
-----------------------------------------------------------------------------------------------------------------

MATEMÁTICA

MEDINA VANINA

NÚMEROS NATURALES. PARTE 2. POTENCIACIÓN Y PROPIEDADES

Buenas tardes 1° F, les adjunto la clase de números naturales, segunda parte.
El día viernes estaré respondiendo dudas sobre ésta clase, si no llega a ver dudas, continuaremos con el tema.
Recuerden escribirme:                       vaninamedinasecundaria@gmail.com

Números naturales (potenciación y sus propiedades)

Copiamos el siguiente concepto en la carpeta:

5²

5: es la base

2: es el exponente

POTENCIACION: es una operación que permite escribir en forma abreviada una multiplicación de factores iguales.

 4²= 4 . 4 = 16 “cuatro elevado al cuadrado”
4³= 4 . 4 . 4 = 64 “cuatro elevado al cubo”

IMPORTANTE!!

“Todo número elevado a la cero da como resultado uno”

   2⁰= 1

“Todo número elevado a la uno, da como resultado ese mismo número”

  6¹ = 6           8¹ = 8

ACTIVIDAD 1: Completen la tabla. Tengan en cuenta el primer ejemplo resuelto

POTENCIA	DESARROLLO	RESULTADO
72	7 . 7	49
23		8
	3 . 3 . 3 . 3
82		64
	6 . 6. 6 . 6 . 6
92		81
103
122		144

        

ACTIVIDAD 2: escriban como potencia los siguientes productos y resuelvan. Tengan en cuenta el primer ejemplo resuelto

a)       ___ ---   = 5 .5 .5 = ____

b)      ___ ---   = 2 . 2 . 2 . 2 . 2 . 2  = ____

c)      ___ ---   = 3 . 3 = ____

d)      ___ ---   = 7 . 7 . 7  = ____

e)      ___ ---   = 6 . 6 . 6 . 6  = ____

f)       ___ ---   = 9 . 9 . 9  = ____

5³= 5 . 5. 5 = 125 Deben completar la base, exponente y el resultado. 

ACTIVIDAD 3: completen las tablas. Lo que está con rojo son ejemplos de cómo deben resolver

A)

N	0	1	2	3	4	5	6	7	8	9	10
N2	02 = 0	12  = 1

B)

N	0	1	2	3	4	5	6	7	8	9	10
N3	03  = 0	13  = 1

Propiedades de la potenciación:

Ingresamos al siguiente link: https://youtu.be/Gh0jcNkas2g

Luego de mirar el video copiamos el siguiente cuadro con ejemplos:

Propiedades de la potenciación	Ejemplo
Propiedad 1:Para multiplicar dos potencias de igual base, se escribe la misma base y se suman los exponentes.	32 . 33 = 32+3 = 35
Propiedad 2:Para dividir dos potencias de igual base, se escribe la misma base y se restan los exponentes.	25 : 22 = 25 - 2 = 23
Propiedad 3:Para calcular la potencia de otra potencia, se escribe la misma base y se multiplican los exponentes.	(52)3 = 52 . 3 = 56

Propiedad 4: “La potenciación es distributiva con respecto a la multiplicación y a la división”

SIN APLICAR LA PROPIEDAD	APLICANDO LA PROPIEDAD
(4.3)2 Resolvemos primero el paréntesis y luego calculamos la potencia   122= 12.12=144	(4.3)2 Elevamos cada número por separado al exponente y después multiplicamos los resultados     42 . 32= 16.9= 144
(12:4)2 Resolvemos primero el paréntesis y luego calculamos la potencia           32 =9	(12:4)2 Elevamos cada número por separado al exponente y después dividimos los resultados 122 : 42=144:16=9

CONCLUSIÓN: Al resolver de dos formas distintas, vemos que da el mismo resultado, entonces podemos afirmar que la potenciación es distributiva respecto de la multiplicación y de la división.

IMPORTANTE!!!!

“LA POTENCIACIÓN NO ES DISTRIBUTIVA RESPECTO A LA SUMA Y A LA RESTA”

(No puedo distribuir el exponente cuando dentro del paréntesis tengo suma o resta)

Veamos algunos ejemplos en el siguiente cuadro para demostrar ésto.

Forma correcta de resolver	Forma incorrecta de resolver
Resolvemos la suma o resta que tenemos dentro del paréntesis y luego calculamos la potencia. (6+3)2=92=81 (10-6)2=42=16	De la siguiente forma no puedo resolverlo (6 + 3)2= 62+32=36+9=45(mal) (10 - 6)2=102-62=100-36=64(mal)

CONCLUSION:

-La potenciación si es distributiva respecto de la multiplicación y de la división.

-La potenciación no es distributiva respecto de la suma y de la resta.

Actividad 4: Resolver aplicando propiedades, cuando sea posible

A)    4 . 4² . 4² . 4⁰=

B)    14¹² : 14¹⁰ . 14=

C)    5⁵³ : 5¹⁷ . 5²⁸ : 5⁶³=

D)    (2²)²  .  2³=

E)     (7  .  5)³=

F)     (18 . 2 : 9)²=

G)    (7 + 2)³=

H)    (12 - 6)²=

----------------------------------------------------------------------------------------------------------

Cursos 1° F y 1° E    TP 23-04

Construcción de la Ciudadania -  T.Tarde

Prof. Nora Salias

Espero que se encuentren bien! , les adjunto la actividad grupal de la semana reitero los que puedan ingresar a Classroom , realizan un documento y lo suben por Tarea de Clase.

¿QUE SIGNIFICA SER CIUDADANO?

¿En qué piensan ustedes cuando les preguntan si son ciudadanos? ¿En si

tienen la nacionalidad de este país? ¿En si pueden votar? ¿O en otras cosas, como si pueden acceder a derechos  de los que supuestamente gozan los habitantes de nuestra nación? ¿O si pueden participar en cambiar las cosas que creen que no están bien en donde viven?

Todas estas preguntas parten de diferentes conceptos de ciudadanía.

En la República Argentina seguimos teniendo vigente, con modificaciones,

una ley de ciudadanía de 1869 (la Ley 346), que establece que son argentinos

todos los nacidos en este territorio (salvo los hijos de diplomáticos),

los hijos de argentinos que hayan nacido en el extranjero y que opten

por la ciudadanía de origen, y todos los extranjeros mayores de edad con

residencia de al menos dos años y de buena conducta que quieran hacer el trámite de ciudadanía

por naturalización. Es decir que en esta ley se conjugan los conceptos de ciudadanía y nacionalidad.

La ciudadanía se refiere a la inclusión de una persona en un Estado determinado, y al compromiso

mutuo de deberes y derechos. La nacionalidad tiene que ver con el lugar de nacimiento de cada

uno, o del nacimiento de sus ancestros, y también está relacionada con la ciudadanía que se adopta  y con el universo cultural que uno considera propio. Por ejemplo, muchos jóvenes argentinos hijos de bolivianos se sienten argentinos, y algunos se pueden considerar bolivianos; así como jóvenes nacidos durante el exilio de sus padres en el extranjero se pueden considerar argentinos o de doble nacionalidad. Es decir, la nacionalidad tiene que ver con lo que se siente que es la patria.

                                                                           LECTURA

¿Cómo puedo saber cuál es mi patria?

El primero respondió:

—Patria es la tierra donde tiene uno echadas las raíces, cuya voz profunda llama a la propia

sangre cuando se está fuera de ella.

—Pero también –protestó el segundo– y tal vez ante todo, “patria” tiene que ser el suelo en

donde uno puede sembrar porque hay una franja de ella en que se le permite hacerlo.

Dijo entonces el tercero:

—Las dos cosas me parecen bien, aunque supongo que “patria” tiene que ser además una

dimensión común con otras personas queridas con las que se pueda compartir el camino, la

fatiga y el disfrute, por aquello que dicen las Escrituras:

“tengo mis raíces donde mi corazón se reconforta, y mi sendero conduce a una cima a la que

solo se puede llegar acompañado”.

                                   Conrado Eggers Lan, 1985, primera Navidad en Argentina después del exilio

Lectura:

Actividades

1 ¿Cuáles son los distintos conceptos de patria que se tratan en esta selección?

2 Averigüen entre tus mayores cuál es su patria y pregunten las razones por las cuales

sostienen eso.

3 Busquen otras definiciones de “patria”. Elijan la que más les guste. Justifiquen su

respuesta.

4  Comenten un libro o una película que puedan relacionar con el concepto de ciudadano.

Bueno espero sus trabajos , quiero que se cuiden mucho  , un abrazo virtual

                                                                         Prof.Nora

--------------------------------------------------------------------------------------------------------------------------

MATEMÁTICA

MEDINA VANINA

Hola 1° F, les escribo la clase de potenciación y propiedades, los ejercicios resueltos, recuerden que si tienen alguna duda, deben escribirme a vaninamedinasecundaria@gmail.com.

En la semana estaré subiendo la clase de Radicación y propiedades 

Saludos 

RESPUESTAS 

ACTIVIDAD 1: Completen la tabla. Tengan en cuenta el primer ejemplo resuelto

POTENCIA	DESARROLLO	RESULTADO
72	7 . 7	49
23	2.2.2	8
3⁴	3 . 3 . 3 . 3	81
82	8.8	64
6⁵	6 . 6. 6 . 6 . 6	7776
92	9.9	81
103	10.10.10	1000
122	12.12	144

ACTIVIDAD 2: escriban como potencia los siguientes productos y resuelvan. Tengan en cuenta el primer ejemplo resuelto

A) 5 ᵌ = 5 . 5 . 5 = 125

B) 2 ⁶ = 2. 2. 2. 2. 2. 2 = 64

C) 3² = 3.3 = 9

D)                       7ᵌ = 7.7.7= 343

E)  6⁴=6.6.6.6=1296

F)  9ᵌ = 9.9.9=729

ACTIVIDAD 3: completen las tablas. Lo que está con rojo son ejemplos de cómo deben resolver

N	0	1	2	3	4	5	6	7	8	9	10
N2	02 = 0	12  = 1	4	9	16	25	36	49	64	81	100

N	0	1	2	3	4	5	6	7	8	9	10
N3	03  = 0	13  = 1	8	27	64	125	216	343	512	729	1000

Actividad 4: Resolver aplicando propiedades, cuando sea posible

A)    4 . 4² . 4² . 4⁰=

COMO ES MULTIPLICACIÓN SE SUMAN TODOS LOS EXPONENTES

4⁵= 1024

B)14¹² : 14¹⁰ . 14=

RESTO Y SUMO LOS EXPONENTES : 12 -10+1= 3

14ᵌ =2744

C)    5⁵³ : 5¹⁷ . 5²⁸ : 5⁶³=

RESTO Y SUMO LOS EXPONENTES : 53-17+28-63 =1

5¹ = 5

D)    (2²)²  .  2³=

MULTIPLICO LOS EXPONENTES, POTENCIA DE OTRA POTENCIA 2 .2 = 4

2⁴ . 2ᵌ = LUEGO SUMO LOS EXPONENTES: 4 + 3

2⁷= 128

E)     (7  .  5)³=

APLICO PROPIEDAD DISTRIBUTIVA

7ᵌ . 5ᵌ = LUEGO RESUELVO, NO SE PUEDEN SUMAR LOS EXPONENTES PORQUE SON DE DIFERENTES BASES

343                       125 = 42.875

F)     (18 . 2 : 9)²=

APLICO PROPIEDAD DISTRIBUTIVA

18² . 2² : 9² = LUEGO RESUELVO

 324 . 4 . 81 = 16

G)     (7 + 2)³= NO SE PUEDE APLICAR PROPIEDAD DISTRIBUTIVA, YA QUE HAY UNA SUMA ENTRE EL 7 Y EL 2, ENTONCES PRIMERO RESULVO EL PARÉNTESIS Y LUEGO LA POTENCIACIÓN

9² = 81

H)     (12 - 6)²= NO SE PUEDE APLICAR PROPIEDAD DISTRIBUTIVA, YA QUE HAY UNA RESTA  ENTRE EL 12  Y EL 6 , ENTONCES PRIMERO RESULVO EL PARÉNTESIS Y LUEGO LA POTENCIACIÓN

6² = 36

-------------------------------------------------------------------------------------------------------------------------

Cursos 1° F y 1° E    TP 30-04

Construcción de la Ciudadania -  T.Tarde

Prof. Nora Salias

Hola a todos!

Espero que se encuentren bien! , les adjunto la actividad grupal de la semana , los que puedan ingresar a Classroom , realizan un documento y lo suben por Tarea de Clase.,.

LA DIGNIDAD HUMANA

La dignidad de las personas La dignidad humana consiste en reconocer que cada persona es merecedora de respeto y de derechos por el solo hecho de ser humano, sin importar sus condiciones o características propias. El reconocimiento y la aceptación de las diferencias hacen a las personas dignas y libres, y confirman la virtud y la propia dignidad del individuo que se basa en el respeto hacia los demás.

La dignidad de las personas

En la actualidad, la democracia, el derecho y la justicia se basan en el principio de la dignidad humana. Esto significa que solamente por el hecho de ser humanos a todas las personas les corresponde, sin ningún tipo de diferenciación, gozar de todos sus derechos. En otras palabras, por su propia naturaleza humana, todas las personas son dignas y merecedoras de respeto. Vivir dignamente consiste entonces en poder satisfacer nuestras necesidades básicas y realizarnos como personas.

1. Buscá en el Diccionario    la palabra “digno”  y leé sus diferentes acepciones.

2. Escribí a continuación dos oraciones empleando los términos “digno” o “dignidad”.

 3. Explicá con tus palabras o con un ejemplo la siguiente afirmación: “La dignidad es un valor que cada ser humano tiene, más allá de su posición social, económica, cultural, de su religión o de su forma de pensar”.

4. Accedé a la Declaración Universal de los Derechos Humanos en la página de las Naciones Unidas: e-sm.com.ar/Decl_DDHH.

a) Buscá y copiá a continuación el artículo 1 de dicha Declaración.

 b) Hacé un dibujo o pegá una foto en otra hoja que ilustre el contenido de dicha norma.

¿Qué título le pondrías? Escribilo debajo.

Les pido que tengamos en cuenta lo que escribo  aquí:

Todos los seres humanos ,  merecen ser respetados

Sin distinción                            Solo por ser personas

La dignidad humana es la base de los Derechos Humanos

Los Derechos Humanos  son  Innatos  Universales  Irrenunciables  Inviolables  Indivisibles

Se clasifican en     Civiles Políticos Económicos, sociales y culturales De solidaridad  

Les cuento que esta semana les envio el trabajo en dia viernes por problemas con la computadora.

Espero que estén bien , les mando un abrazo grande  y  a trabajar.

                                                                                                                Prof.  Nora

EDUCACIÓN  ARTÍSTICA (PLÁSTICA) 1°F T.T

PROFESORA :ROSA BEATRIZ GIMENEZ

NUEVA TAREA :" DIA DE LA TIERRA"  

HOLA CHICOS ,EL 22 DE ABRIL SE CELEBRO EL DÍA DE LA TIERRA.

REALIZARAN  UNA BREVE REFLEXIÓN CON UN DIBUJO. ES DECIR,HACER UN DIBUJO

REFERENTE A NUESTRO PLANETA  Y ESCRIBIRLE UNA REFLEXIÓN.SE ENTREGA LA SEMANA QUE VIENE.

LES DEJO ALGUNAS IMÁGENES COMO EJEMPLOS.

SALUDOS. PROFESORA  DE PLÁSTICA.
  CUÍDENSE  MUCHO

   

-----------------------------------------------------

Ed. Física

Código de classroom: 7vwnumz

--------------------------------------------------------------------------------

MATEMÁTICA

MEDINA VANINA

CLASE: RADICACIÓN Y PROPIEDADES

Hola 1° f les adjunto la clase, tienen actividades. Cualquier duda me consultan a vaninamedinasecundaria@gmail.com 
Saludos!!!

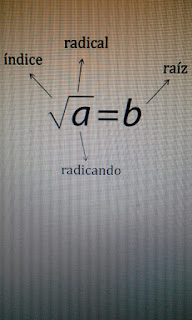
RADICACIÓN

En la Radicación intervienen símbolos que debemos tener en cuenta en cuanto a su significado:

Existen distintos tipos de raíces:

·         Raíz cuadrada, en la misma el índice es 2, pero suele NO ESCRIBIRSE. Es decir, cuando el índice no está escrito, es porque se trata del índice 2, e implica una raíz cuadrada.

·         Raíz cúbica, en la cual el índice es 3.

·         Raíz cuarta, en la cual el índice es 4.

Y así sucesivamente, en adelante serán raíces quintas, sextas, séptimas, etc., para los índices 5, 6, 7, etc., respectivamente.

Pero… ¿Qué es la Radicación?...

Es decir que está relacionada con el tema anteriormente visto, que es la Potenciación.

Cuando hablamos de la raíz de un número, nos referimos a “de dónde viene ese número”, “cuál es su raíz”, “cuál es su origen”.

VAMOS CON ALGUNOS EJEMPLOS

ü  Por esto, si nos preguntamos cuál es la raíz cuadrada (cuadrado se refiere al índice 2, al hecho de haber multiplicado a un número por sí mismo 2 veces) de 49, nos estamos preguntando: ¿Cuál es el número al cuál multipliqué 2 veces por sí mismo, para que el resultado me haya dado 49? Si pruebo con 2, por ejemplo, y realizo 2.2 me da 4, entonces el 2 NO es el número buscado. Si pruebo con el 3 y hago 3.3 esto me da 9, entonces el 3 NO es el número buscado. Así puedo ir probando hasta que llego al 7, y hago 7.7 (multiplico al 7 dos veces por sí mismo) y esa cuenta da 49. ¡¡¡¡Claro, entonces el número buscado es 7!!!! Por esto, la raíz CUADRADA de 49 es 7.

ü  Cuando me pregunto ¿Cuál es la raíz CÚBICA (cubo hace referencia al 3, entonces se trata de una raíz de índice 3) de 64? Debo preguntarme: ¿cuál es el número que multiplico 3 veces por sí mismo para que el resultado obtenido sea 64? Puedo ir probando. Si lo hago con 2, entonces 2.2.2 es 8 con lo cual 2 NO es el número buscado. Si pruebo con el 3, debo hacer 3.3.3 lo cual me da 27, entonces el 3 NO es el número buscado. Si pruebo con 4 y hago 4.4.4 (multiplico al 4  3 veces por sí mismo) esto me da 64. ¡¡¡¡Entonces la raíz cúbica de 64 es el 4!!!!

Tanto para encontrar la raíz cuadrada de 49, como la raíz cúbica de 64, puedo observar la tabla realizada en la clase pasada sobre “Potenciación y sus Propiedades”. En la tabla de los cuadrados puedo analizar las raíces cuadradas. Y por lo tanto en la tabla de los cubos, puedo encontrar las raíces cúbicas. Te propongo analizarlo antes de pasar a las actividades.

Actividades

1   1) Completen con los números que faltan:

 PROPIEDADES DE LA RADICACIÓN

Al igual que la Potenciación, la Radicación posee ciertas Propiedades, es decir formas alternativas de resolver un cálculo de una manera diferente, pero llegando al mismo resultado.

Veamos el siguiente cuadro:

En la primera fila podemos ver que las raíces se pueden “repartir” o “separar”, siempre que se trate de una multiplicación o una división, ello nos permite obtener los resultados más fácil y rápidamente.

Para mayor información puedes consultar el video tutorial (hasta el minuto 3:40 es suficiente)  https://www.youtube.com/watch?v=dT6BcSrH4q0

Entonces, ahora sí estás listo para resolver las siguientes actividades.

1  2)  Resuelve aplicando propiedades cuando sea posible

1  3) Coloca V o F y JUSTIFICA (puedes hacer las cuentas o bien justificar según lo que establecen las propiedades de la radicación)

---------------------------------------------------------------------------------------------------------------------------

MATEMÁTICA

MEDINA VANINA

CLASE: CLAVE DE CORRECCIÓN RADICACIÓN Y PROPIEDADES

Hola 1° f les adjunto la clase correspondiente a la clave de corrección. Cualquier duda que tengan o diferencia me consulta a vaninamedinasecundaria@gmail.com
Saludos 

---------------------------------------------------------



1°F  (T. T ) ARTÍSTICA (PLÁSTICA)
PROFESORA ROSA GIMENEZ
 NUEVA ACTIVIDAD: 11/5/20

HOMENAJE AL PINTOR QUINQUELA MARTIN

HOLA CHICOS ¿ COMO ESTÁN?.
EN BASE A LO VISTO EN EL VÍDEO DEL MUSEO DE QUINQUELA MARTÍN ,REALIZARAN UN DIBUJO ,DE LO QUE MAS LES GUSTO.
  EJEMPLOS LOS MASCARONES DE PROA, LOS CUADROS DE QUINQUELA, SU PALETA , EL PIANO. ALGÚN LUGAR O ESPACIO QUE LES GUSTO DEL MUSEO QUE A SU VEZ ERA LA CASA DEL ARTISTA.

EN LO POSIBLE USEN TEMPERAS PARA TRABAJAR. LES DEJO ALGUNAS PINTURAS ,POR SI QUIEREN HACERLAS,IGUAL TIENEN VARIAS OPCIONES.
SALUDOS
PROFESORA ROSA GIMENEZ.

POR FAVOR ,PARA QUIENES NO ENTREGARON NADA ,PONERSE AL DÍA CON LAS TAREAS.

ACTIVIDAD  Semana del   06-05

CCD    1° F y  1° E      T.T 

Prof. Nora  Salias

Hola a todos, para  la actividad de hoy tiene  les pido que presten atención a todas las pautas que les planteo para poder realizar bien la tarea .

Vigencia de los derechos humanos

Los Estados tienen la obligación de proteger, promover y hacer cumplir los derechos de sus habitantes mediante acciones que les brinden la posibilidad de hacer efectivos sus derechos. Y deben abstenerse de tomar medidas que limiten el libre ejercicio de estos. El ámbito ideal para ello es el sistema democrático, ya que solamente en un marco que proteja los principios de la libertad y de la igualdad ante la ley es posible llevar adelante políticas que promuevan la plena vigencia de los derechos humanos.

1. Buscá en diarios digitales o impresos una noticia que ejemplifique la vigencia o el incumplimiento de algún derecho en nuestro país.

 a) Subrayá las ideas principales y escribí a partir de ellas un resumen de la noticia.

 b) Señalá el derecho al que se refiere la noticia y explicá de qué manera aparece respetado o afectado, según sea el caso.

c) Escribí debajo un nuevo título para la misma noticia.

d) En grupos, hagan una puesta en común a partir de sus trabajos y expresen su opinión sobre las distintas problemáticas que se planteen.

2. Vean en el aula la película Pa-ra-da (2008) que plantea la problemática de los chicos de la calle. Luego de verla, organicen un debate a partir de las siguientes preguntas. a) ¿Reconocen situaciones de “indiferencia” en su vida cotidiana? b) ¿Qué otros grupos, además de los niños, piensan que son víctimas de la indiferencia social? c) ¿Qué acciones realizan o podrían realizar ustedes para cambiar la realidad que se muestra en el filme?

3. Observá los siguientes cuadros del pintor santafesino Antonio Berni: Juanito Laguna dormido (1974) y Juanito Laguna va a la fábrica (1977). a) ¿De qué manera los relacionarían con el tema de la vigencia de los derechos humanos? b) Escribí para cada uno un epígrafe que los relacione.

Bueno ya saben que nos seguimos cuidando en casa , pero les pido que hagan los ejercicios  , cualquier cosa me consultan por classroom. , un abrazo virtual  . Prof.Nora

1°F  EDUCACIÓN ARTÍSTICA (PLÁSTICA)

HOLA CHICOS,LES DEJO UN VÍDEO DEL PINTOR ARGENTINO  :BENITO QUINQUELA MARTÍN.

ESCUCHEN SU BIOGRAFÍA, OBSERVEN  SUS PINTURAS Y TÉCNICAS. EN BASE A ESTO LA SEMANA QUE VIENE REALIZAREMOS UNA ACTIVIDAD EN LA CARPETA.
CUÍDENSE MUCHO. Les dejo el link ⇓

MUSEO QUINQUELA MARTÍN


POR FAVOR ENTREGAR LAS TAREAS DADAS  HASTA EL MOMENTO.
YA QUE MUCHOS TODAVÍA ,NO LAS HAN ENTREGADO Y TAMPOCO SE HAN COMUNICADO.
SALUDOS. 
PROFESORA ROSA GIMENEZ.

---------------------------------------------------------
Construcción de Ciudadanía

Nuevo código de classroom: f72nfy6
---------------------------------------------------------

MATEMÁTICA

MEDINA VANINA

CLASE: OPERACIONES COMBINADAS 

Hola 1° f les adjunto la clase correspondiente OPERACIONES COMBINADAS. Cualquier duda que tengan  me consultan a vaninamedinasecundaria@gmail.com De cada ejemplo hay un video explicativo. 

OPERACIONES COMBINADAS EN LOS NÚMEROS NATURALES

Vamos a combinar las 6 operaciones que conocemos hasta el momento: suma, resta, multiplicación, división, potenciación y radicación.

Cuando estas 6 operaciones se combinan en un mismo cálculo, se deben respetar ciertas reglas que establecen el orden en que debemos operar, es decir, hacer las cuentas.

EJEMPLO 1:

·        Para resolver una operación combinando todas las operaciones, se pueden seguir los siguientes pasos:

1)     Se separa en términos.

2)     Se resuelven las potencias y raíces (aplicando las propiedades cuando sea posible).

3)     Se resuelven las multiplicaciones y divisiones.

4)     Se resuelven las sumas y las restas.

Ver la resolución del ejemplo 1 en el siguiente link: https://youtu.be/lu8CYqTWIHI

EJEMPLO 2:

·        Para resolver una operación combinada donde aparecen paréntesis, se pueden seguir los siguientes pasos:

1)     Se separa en términos.

2)     Se resuelven las operaciones encerradas en los paréntesis (separando en términos).

3)     Se resuelve respetando la jerarquía (orden) de las operaciones.

Ver la resolución del ejemplo 2 en el siguiente link: https://youtu.be/_ic1OVeXv30

EJEMPLO 3:

·        Si hay operaciones en el radicando o como base de una potenciación, se deben resolver antes de calcular la raíz o la potencia.

1)     Se separan en términos.

2)     Se resuelven las operaciones que hay en el radicando y en la base de la potencia respetando la jerarquía (orden).

3)     Se resuelven las potencias y las raíces.

4)     Se resuelven las sumas y las restas.

Este mismo ejemplo 3, está explicado en el siguiente link: https://youtu.be/BvJPLbjxIAk

ACTIVIDADES:

1)     Respondan y expliquen las respuestas.

a)      ¿Cuál es el resultado de 4.(100 – 50.2)?

b)     ¿Cuál es el resultado de 45 – 5.8? 

c)      ¿Cuál es el resultado de 10 + 30:5?

2)     Resolver los siguientes cálculos. 

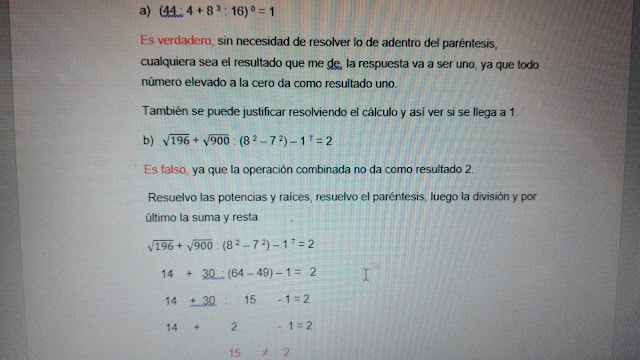
1)     Decide V (verdadero) o F (falso) y justifica tu respuesta.

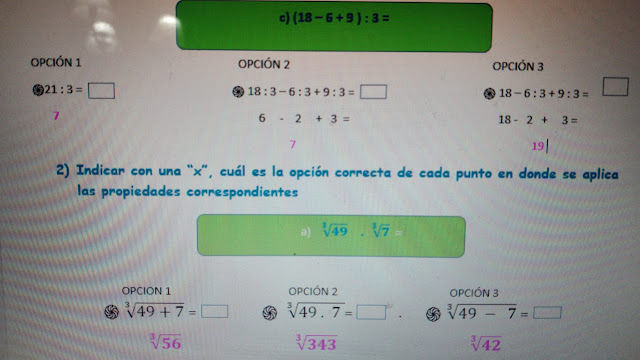
1)     Resuelve aplicando propiedades de la potenciación y la radicación, cuando sea posible

--------------------------------------------------------

MATEMÁTICA

MEDINA VANINA

CLASE: CLAVE DE CORRECCIÓN - OPERACIONES COMBINADAS 

Hola 1° f les adjunto la clase correspondiente A LA CLAVE DE CORRECCIÓN DE OPERACIONES COMBINADAS  Cualquier duda o diferencia que tengan  me consultan a vaninamedinasecundaria@gmail.com.
El día viernes estaré enviando una clase de integración de contenidos, la cual deberán entregar el martes 02/06/2020 para cerrar el trimestre. 

Clave de corrección. Operaciones combinadas con números naturales.

ACTIVIDADES:

1)    Respondan y expliquen las respuestas.

a)    ¿Cuál es el resultado de 4.(100 – 50.2)?

El resultado es cero.

Puedo resolverlo mediante dos procedimientos.

Primer procedimiento:

·         Separo en términos adentro del paréntesis.

·         Resuelvo la multiplicación 50 . 2

·         Resuelvo la resta.

·         Por ultimo multiplico los dos números que quedan.

    4 . ( 100 – 50 . 2 ) =

    4 . ( 100 – 100 ) =

    4 . 0 = 0

            Segundo procedimiento: una vez que resuelvo la multiplicación que esta adentro del paréntesis, puedo aplicar propiedad distributiva.

 4 . ( 100 – 50 . 2 ) =

 4 . ( 100 – 100 ) =

 4 . 100 – 4 . 100 =

 400 – 400 = 0

b)    ¿Cuál es el resultado de 45 – 5.8? 

El resultado es 5.

Separo en términos, luego resuelvo la multiplicación y por último la resta.

45 – 5 . 8 =

45 – 40 = 5

c)    ¿Cuál es el resultado de 10 + 30:5?

El resultado es 16.

Se separa en términos, resuelvo la división y por último sumo.

10 + 30 : 5 =

10 + 6 = 16

2)    Resolver los siguientes cálculos.

1)    Decide V (verdadero) o F (falso) y justifica tu respuesta.

1)    Resuelve aplicando propiedades de la potenciación y de la radicación.

--------------------------------------------------------

MATEMÁTICA

MEDINA VANINA

CLASE: CLASE DE INTEGRACIÓN DE CONTENIDOS. CIERRE DEL TRIMESTRE
LAS ACTIVIDADES QUE FIGURAN EN ÉSTA CLASE LA DEBEN ENTREGAR PARA EL MARTES 02/06/2020

1°F ARTÍSTICA PLÁSTICA
PROFESORA:  Rosa Gimenez

NUEVA ACTIVIDAD: N°10

COMPOSICIÓN LIBRE CON LOS ELEMENTOS QUE TENGAN EN CASA.
Saludos y cuídense mucho.☺

• Chicos es importante que realicen y envíen las tareas antes de este viernes
• Hay muchos alumnos que no se comunican, ni envían nada.

------------------------------------------------------------------------------------------------------------------

PRÁCTICAS DEL LENGUAJE

CÓDIGO CLASSROOM: fpvqgig

-------------------------------------------------------------------------------------------------------------------
MATEMÁTICA 
FECHA: 12/06/2020

CLASE: 1

TEMA: LENGUAJE COLOQUIAL Y SIMBÓLICO

Hola 1° F  les adjunto la clase correspondiente a lenguaje coloquial y simbólico. 
Con ésta clase estamos comenzando con el 2° trimestre
Cualquier duda me escriben a vaninamedinasecundaria@gmail.com 

Lenguaje coloquial y simbólico.

Ingresamos al siguiente link:

 https://www.youtube.com/watch?v=WnlfTyMDi-I&feature=share

Luego de mirar el video copiamos lo siguiente en la carpeta:

El lenguaje de las palabras, que puede ser oral o escrito, se denomina lenguaje coloquial. La matemática utiliza un lenguaje particular denominado lenguaje simbólico.

Tener en cuenta que las letras representan un número cualquiera.

Lenguaje coloquial	Lenguaje simbólico
El doble de cinco	2 . 5
El doble de un número cualquiera	2 . n = 2n
La mitad de ocho	8 : 2
La mitad de un número cualquiera	r : 2
El siguiente de un número cualquiera	p + 1
El triple de un número	3 . x = 3x
La cuarta parte de un número	a : 4
El anterior de un número	b – 1
El doble de un número, disminuido en cuatro	2 . x – 4
El siguiente del doble de un número	2 . n + 1
El doble del siguiente de un número	2 . (n + 1)
La diferencia entre ocho y dos	8 – 2
El producto entre seis y cuatro	6 . 4
El cociente entre veinte y cinco	20 : 5

Si entre un número y la letra no se indica la operación, se entiende que hay un signo de multiplicar.

                              6 . x = 6x

ACTIVIDADES:

ACTIVIDAD 1: Traducir al lenguaje simbólico y resolver. (el primero se da de ejemplo)

Lenguaje coloquial	Lenguaje simbólico
La suma entre nueve y once	9 + 11 = 20
El triple de catorce
La diferencia entre el cien y el treinta y nueve
El producto entre siete y ocho
La suma entre veinticuatro y setenta y dos
La mitad de noventa y dos
El cociente entre el treinta y el seis

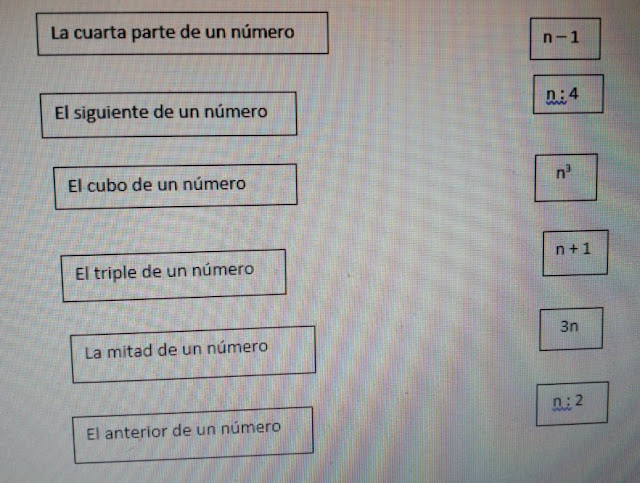
ACTIVIDAD 2: Unir cada expresión coloquial con su expresión simbólica.

ACTIVIDAD 3: Traducir a lenguaje coloquial las siguientes expresiones simbólicas.

a)    12 – 5

b)    40 : 8

c)    7 . 4

d)    200 : 2

e)    2.n – 1

f)     2.n + 1

g)    2 . (n + 1)

----------------------------------------------------------------------------------------------------------------------

MATEMÁTICA 
FECHA: 17/06/2020

CLASE: 2

TEMA: CLAVE DE CORRECCIÓN, correspondiente a la clase de lenguaje coloquial y simbólico 

Hola 1° F  les adjunto la clase n° 2  


Cualquier duda me escriben a vaninamedinasecundaria@gmail.com 

ACTIVIDAD 1: Traducir al lenguaje simbólico y resolver. (el primero se da de ejemplo)

Lenguaje coloquial	Lenguaje simbólico
La suma entre nueve y once	9 + 11 = 20
El triple de catorce	3.14 = 42
La diferencia entre el cien y el treinta y nueve	100 – 39
El producto entre siete y ocho	7.8 = 56
La suma entre veinticuatro y setenta y dos	24 + 72 = 96
La mitad de noventa y dos	92 : 2 = 46
El cociente entre el treinta y el seis	30 : 6 = 5

ACTIVIDAD 2: Unir cada expresión coloquial con su expresión simbólica.

ACTIVIDAD 3: Traducir a lenguaje coloquial las siguientes expresiones simbólicas.

a)    12 – 5            La diferencia entre doce y cinco

b)    40 : 8              El cociente entre el cuarenta y el ocho

c)    7 . 4                El producto entre siete y cuatro

d)    200 : 2           La mitad de doscientos

e)    2.n – 1           El anterior del doble de un número

f)     2.n + 1           El siguiente del doble de un número

g)    2 . (n + 1)      El doble del siguiente de un número

Aclaración: en el punto 3.d. también se puede decir “el cociente entre doscientos y dos”, pero al tratarse de la división por dos, siempre se traduce a la palabra “mitad”, por ello es más específico hablar de “la mitad de doscientos”.

--------------------------------------------------------------------------------------------------------------------------

MATEMÁTICA 
FECHA: 19/06/2020

CLASE: 3

TEMA: ECUACIONES 

Hola 1° F  les adjunto la clase n° 3  



Cualquier duda me escriben a vaninamedinasecundaria@gmail.com

LENGUAJE SIMBÓLICO. ECUACIONES

Te propongo los siguientes acertijos:
1) ¿Cuál es el número al cual se le resta 3 y da como resultado 20? El número es_______
2) ¿Cuál es el número que al sumarle 3 da como resultado 12? El número es_______
3) ¿Cuál es el número al cual se lo multiplica por 6 y da como resultado 42? El número es_____
4) ¿A qué número se lo divide por 5 y su resultado es 8? El número es _____

Los números, que en cada pregunta, cumplen con lo pedido son las soluciones a cada problema planteado. Ahora bien, cada uno de esos problemas está expresado en LENGUAJE COLOQUIAL (Lenguaje comúnmente hablado) y se pueden escribir en el lenguaje propio de la Matemática, que es el LENGUAJE SIMBÓLICO.
Entonces volvamos a leer la pregunta 1.

1) ¿Cuál es el número al cual se le resta 3 y da como resultado 20? 
Cuando hay un número desconocido, lo podemos representar con alguna letra, la que fuera. Generalmente se representa con una x cuando tenemos un valor que no conocemos. Si planteamos esta pregunta en Lenguaje Simbólico, queda expresado así:
x – 3 = 20
Ahora podemos probar con algún número, si tu respuesta al comienzo fue que x vale 23, estás en lo cierto pues:
23 – 3 = 20
El “23” es la Solución de este problema.

Si hubieses probado, por ejemplo con 18: 18 – 3 da 15, no da 20, entonces el “18” NO ES solución del problema.

2) ¿Cuál es el número que al sumarle 3 da como resultado 12? 
Planteemos esta pregunta en Lenguaje Simbólico:
x + 3 = 12
Probemos, si x toma el valor 9, entonces la igualdad se cumple
9 + 3 = 12
El “9” es la solución al problema
3) ¿Cuál es el número al cual se lo multiplica por 6 y da como resultado 42? 
En Lenguaje Simbólico:
x . 6 = 42
Probemos, si pensaste en el 7, es correcto, pues:
7 . 6 = 42
El “7” es la solución al problema.


4) ¿A qué número se lo divide por 5 y su resultado es 8? 
En Lenguaje Simbólico:
x: 5 = 8
El número x es el 40, pues 40 : 5 es lo que da 8
40 : 5 = 8
Entonces “40” es la Solución al problema.


Observen que en los cuatro planteos anteriores escritos en Lenguaje Simbólico, interviene un valor desconocido, al cual se lo llama “incógnita”, y lo escribimos con la letra x, y una igualdad. Las expresiones de este tipo tienen un nombre específico, y se denominan, a partir de este momento ECUACIONES.

¡Te propongo el siguiente juego, a ver si sale!!

Debes encontrar los valores de cada figura, tenes 3 pistas que servirán de ayuda

 Algunas preguntas….

¿Cómo lograron  hallar el valor del   KOALA    ?

¿Cómo hallaron el valor del    OSO ?

¿Cuáles serían las incógnitas en éste caso? 

¿Cuáles serían las incógnitas en éste caso? 

ACTIVIDAD  1:

Escribe cada problema como una ecuación, tal como se muestra en el ejemplo, y encuentra el número que cumple con la condición.

A)    A un número se le resta 4 y da como resultado 8. ¿Cuál es el número?

x– 4 = 8          El número es 12

B)    A un número se le suma 13 y da como resultado 14. ¿Cuál es el número?

C)    A un número se le busca el doble y su resultado es 24. ¿Cuál es el número?

D)    A un número se lo divide por 5 y su resultado es 5. ¿Cuál es el número?

ECUACIONES. DEFINICIÓN.

Una ecuación es una igualdad en la que hay, por lo menos, un valor desconocido llamado incógnita.

Y además, todo lo que está antes del símbolo de igualdad se llama Primer Miembro, y lo que está después, se llama Segundo Miembro.

Con las ecuaciones ocurre algo parecido, pero en este caso es NECESARIO que ese equilibrio (equivalencia) se mantenga siempre, pues no todas las ecuaciones son tan sencillas de resolver como las que venimos haciendo hasta ahora.

ECUACIONES. RESOLUCIÓN

Resolver una ecuación es encontrar el o los valores de la incógnita que hacen verdadera la igualdad. Cada valor de la incógnita es una solución de la ecuación.

Para resolver una ecuación se pueden obtener ecuaciones equivalentes, es decir con la misma solución, teniendo en cuenta las siguientes propiedades:

·         Se suma o resta un mismo número a ambos miembros de la igualdad (se hace lo mismo de un lado y del otro)

·         Se multiplica o divide por un mismo número (distinto de cero) a ambos miembros de la igualdad (se hace lo mismo de un lado y del otro)

·         Se aplica una potencia o raíz a ambos miembros de la igualdad (se hace lo mismo de un lado y del otro)

Ahora sí, vamos a resolver las mismas ecuaciones del comienzo, pero con la idea de mantener el “equilibrio”, de respetar la “equivalencia”, que se logra haciendo lo mismo de un lado y del otro de la igualdad. Y lo que haga debe ser lo que me “convenga” hacer. Veamos:

·         En la primera pregunta teníamos:

Lenguaje coloquial: ¿Cuál es el número al cual se le resta 3 y da como resultado 20?

Lenguaje simbólico:   x – 3 = 20

Solución: x = 23

Lo último que falta decir en esta primera parte introductoria sobre Ecuaciones es que, para poder resolverlas, se tratará, SIEMPRE, de lograr que la incógnita quede sola.

En x – 3 = 20 para dejar sola a x, debería poder eliminar el – 3 y para ello debo trabajar con la operación contraria, entonces lo contrario a restar 3, es sumar 3. Recordemos la balanza, si debemos sumar 3, lo tendremos que hacer en ambos miembros, para mantener el equilibrio, así:

Verificación:

Reemplazamos a x por el valor que hallamos como solución, en este caso como x = 40, escribimos nuevamente la ecuación del comienzo con la solución incluida, así:

                                    x : 5 = 8          (escribo nuevamente la ecuación)

                                    40 : 5 = 8        (reemplazo a x por 40)

                                       8     =   8     (se establece una igualdad)

En Conclusión: el valor de la incógnita es correcto, pues al reemplazar a x por 40, se cumple una igualdad entre los miembros, en este caso que 8 = 8.

Solo para que sepas que hacer lo mismo de un lado y del otro de la igualdad es un procedimiento válido para mantener un equilibrio, te cuento que el mismo lleva un nombre y se llama Propiedad Uniforme.

ACTIVIDAD 2.

Plantea nuevamente, para cada ítem de la actividad 1, los siguientes pasos explicados anteriormente, que son:

·         Lenguaje coloquial

·         Lenguaje Simbólico

·         Resolución

·         Solución

·         Verificación

MATEMÁTICA 
FECHA: 24/06/2020

CLASE: 4

TEMA: CLAVE DE CORRECCIÓN. 

Hola 1° F  les adjunto la clase n° 4.   

Cualquier duda me escriben a vaninamedinasecundaria@gmail.com

ACTIVIDAD 1:

Escribe cada problema como una ecuación, tal como se muestra en el ejemplo, y encuentra el número que cumple con la condición.

A) A un número se le resta 4 y da como resultado 8. ¿Cuál es el número?

x– 4 = 8          El número es 12, porque 12 – 4 = 8

B)    A un número se le suma 13 y da como resultado 14. ¿Cuál es el número?

x + 13 = 14     El número es 1, porque 1 + 13 = 14

C)    A un número se le busca el doble y su resultado es 24. ¿Cuál es el número?

2. x = 24         El número es 12, porque 2 . 12 = 24

D)    A un número se lo divide por 5 y su resultado es 5. ¿Cuál es el número?

x : 5 = 5          El número es 25, porque 25 : 5 = 5

 ACTIVIDAD 2.

Plantea nuevamente la actividad 1, tal como se ha mostrado anteriormente, siguiendo estos pasos:

·         Lenguaje coloquial

·         Lenguaje Simbólico

·         Resolución

·         Solución

·         Verificación

Actividad 1.A resuelta como una ecuación

Lenguaje coloquial: A un número se le resta 4 y da como resultado 8. ¿Cuál es el número?

Lenguaje Simbólico: x– 4 = 8

Resolución:                x– 4 = 8                      (se deberá sumar 4 a ambos miembros)

                                    x – 4 + 4 = 8 + 4         (se tachan – 4 con + 4)

                                    x             = 12

Solución:                       x = 12

Verificación:              x – 4 = 8      (se escribe la ecuación)

                                    12 – 4 = 8   (se reemplaza a x por 12 y luego se hacen las cuentas)

                                         8     = 8  (se cumple una igualdad, entonces x = 12 es correcto)

 Actividad 1.B resuelta como una ecuación

Lenguaje coloquial: A un número se le suma 13 y da como resultado 14. ¿Cuál es el número?

Lenguaje Simbólico:   x + 13 = 14

Resolución:                              x + 13 = 14               (se debe restar 13 en ambos miembros)

                                          x + 13 – 13 = 14 – 13       (se cancelan + 13 con – 13)

                                                       x    = 1

Solución:        x = 1

Verificación:                          x + 13 = 14     (se escribe la ecuación)

                                                1 + 13 = 14     (se reemplaza a x por 1 y luego se hacen las cuentas)

                                                     14  = 14    (se cumple una igualdad, entonces x = 1 es correcto)

Actividad 1.C resuelta como una ecuación

Lenguaje coloquial: A un número se le busca el doble y su resultado es 24. ¿Cuál es el número?

Lenguaje Simbólico:                2 . x = 24       (se debe dividir por dos en ambos miembros)

Resolución:                         2 . x : 2 = 24 : 2    (se tachan al 2 que multiplica con el 2 que divide)

                                                  x     = 12

Solución:         x = 12

Verificación:                         2 . x = 24 (se escribe la ecuación)

                                              2 . 12 = 24 (se reemplaza a x por 12 y se hacen las cuentas)

                                                  24   = 24 (se cumple una igualdad, entonces x = 12 es correcto)

Actividad 1.D resuelta como una ecuación

Lenguaje coloquial: A un número se lo divide por 5 y su resultado es 5. ¿Cuál es el número?

Lenguaje Simbólico: x : 5 = 5

Resolución:                            x : 5 = 5          (se deberá multiplicar por 5 en ambos miembros)

                                           x : 5 . 5 = 5 . 5     (se tachan :5 con .5)

                                                     x = 25

Solución:        x = 25

Verificación:                         x : 5 = 5         (se escribe la ecuación)

                                               25 : 5 = 5       (se reemplaza a x por 25 y se hacen las cuentas)

                                                   5    = 5       (se establece una igualdad, entonces x = 25 es correcto)

MATEMÁTICA 

FECHA: 26/06/2020

CLASE: 5

TEMA: ECUACIONES DESPEJE DE INCOGNITA 

Hola 1° F  les adjunto la clase n° 5  

Cualquier duda me escriben a vaninamedinasecundaria@gmail.com

ECUACIONES

DESPEJE DE INCÓGNITAS

Volvamos a una de las ecuaciones de la clase anterior, para analizar el procedimiento y buscar algún método más sencillo de resolución.

EJEMPLO 1

 Paso 1:                                          x – 3 = 20

 Paso 2:                                 x – 3 + 3 = 20 + 3                               

 Paso 3:                               x  - 3 + 3   = 20 + 3       TACHAMOS EL - 3 Y + 3 

 Paso 4:                                           x     = 20 + 3

 Paso 5:                                                 x=  23          

Observen lo que ocurre si se quitan los pasos 2 y 3

 Paso 1:                                         x – 3 = 20

 Paso 4:                                           x     = 20 + 3

 Paso 5:                                               x =  23           

Para ir del Paso 1 al Paso 4, puedo pensar como si el 3 que está restando en el primer miembro, hubiese “pasado” sumando al segundo miembro, es decir que cambiamos de miembro a un número y para ello debemos cambiar la operación principal que está realizando.

Veamos más ejemplos utilizando esta idea.

EJEMPLO 2

                   x. 6 = 42            dejaremos a x sola, entonces observamos al 6 que multiplica   

                       x = 42 : 6      podemos pensar que el 6 “pasa” dividiendo al otro miembro

                       x = 7             luego hacemos el cálculo y listo

EJEMPLO 3

   x : 5 = 8          despejaremos a x, observamos que la acompaña un 5 que la divide

        x = 8 . 5    “pasamos” a ese 5 que realizará la operación contraria, multiplicará

        x = 40       luego hacemos el cálculo y ese es el resultado.

ACTIVIDAD 1

Resuelve, pensando en esta nueva idea de “pasar” los números para despejar a x.

A)    x + 4 = 15

B)    x – 12 = 19

C)    x . 4 = 16

D)    x : 6 = 5

OTROS CASOS

Las ecuaciones no siempre son de este estilo. En muchas ocasiones tenemos con más términos y más operaciones por resolver

EJEMPLO 1

Resolver          x . 2 + 4 = 6 

Pregúntate ahora: ¿A qué número que multiplico por 2 y luego le sumo 4, dará como resultado 6?

El número es… ¡Si, es 1!

Ahora lo resolvemos como una ecuación “pasando” números hacia el otro miembro para dejar sola a x.

 

x . 2   +    4    =    6    

¿Cómo despejamos a x? ¿A quién pasamos primero, al 2 o al 4?

Debes visualizar a x e ir dejándola sola como si se tratara del centro de una cebolla que vas despojando desde las capas más externas hasta llegar al corazón de la misma. Lo primero que se pueden pasar son los términos sin x, pues son términos “libres” de x. Entonces:

 

x . 2   +    4    =    6      “paso” al 4 que suma, restando al otro miembro, pues es un término “libre” de x

x . 2               = 6 – 4     aquí podemos ir haciendo la cuenta 6 – 4 y lo escribimos debajo

x . 2              = 2            ahora lo único que falta “pasar” es el 2 que multiplica a x

x                   = 2:2       despejamos a x y el 2 que estaba multiplicándola pasa dividiendo

x                   =  1         hacemos la división y debajo colocamos el resultado 1

Vemos que el valor de x es lo que ya sabíamos de antemano, que debía dar 1.

Verifiquemos que esto es realmente así:

x . 2   +    4    =    6        copiamos nuevamente la ecuación y luego reemplazamos a x por 1

1 . 2   +  4     =     6       ahora se trata de hacer operaciones simples, recuerda separar en términos

    2     +   4   =     6      vamos haciendo los cálculos siempre hacia abajo

            6       =     6      se muestra una igualdad verdadera, pues es cierto que 6 = 6

Algo importante para decir en este momento es que solo en las ecuaciones debemos “pasar” números para dejar a x sola, pero en la verificación las cuentas se van realizando hacia abajo, hasta llegar a una igualdad verdadera. Si no vemos una igualdad al final de la verificación, indica que hemos cometido un error al resolver la ecuación, o al realizar la verificación, y tendremos que revisar nuestros cálculos.

EJEMPLO 2. Resolvemos la ecuación

3 . x  +  2  =  17              2 es término libre de x, entonces lo puedo pasar primero

3  . x         = 17 – 2         el 2 que antes sumaba, pasará restando

3 . x         =    15             hacemos la resta

     x       = 15 : 3            el 3 que multiplicaba ahora pasa dividiendo

    x        =   5                 la solución de x es 5

Verificamos:

3 . x  +  2  =  17                  escribimos la ecuación

3  . 5    + 2   =    17             reemplazamos la solución 5 en x

15      +   2    =   17             vamos haciendo las cuentas hacia abajo

          17       =   17              encontramos una igualdad verdadera

EJEMPLO 3. Resolvemos la ecuación

                            x :  2 – 4 . 12 =     8         vemos que en el segundo término hay una cuenta para hacer               

                           x : 2  - 48       =      8         entonces hacemos primero 4. 12 que da 48

                                  x : 2        =  8  + 48            el 48 que antes restaba, ahora pasa sumando

                                    x : 2      =      56               hacemos la cuenta 8 + 48 que da 56

                                        x       =       56 .  2        el 2 que antes dividía ahora pasa multiplicando

                                         x      =     112                la solución de x es 112

Verifiquemos

   x : 2 – 4 . 12 =     8       copiamos la ecuación

112:2 – 4 . 12 =     8        reemplazamos a x por la solución que es 112

    56  -    48    =  8           hacemos 112:2 en el primer término y 4. 12 en el segundo  término       

                 8    =  8           la igualdad es verdadera

Aclaración: siempre es necesario separar en términos, y cuando en los términos podamos ir resolviendo algún cálculo antes de “pasar” los números, hay que hacerlos

ACTIVIDAD 2

Resolver y verificar las siguientes ecuaciones

A)    x + 81 – 23 = 204

B)    3.x + 20:4 = 59

C)    5.x + 19 = 64

D)    (x – 31 ) : 11 = 3

MATEMÁTICA 

FECHA: 01/07/2020

CLASE: 6

TEMA: ECUACIONES DESPEJE DE INCOGNITA 

Hola 1° F  les adjunto la clase n° 6 es la continuación de la clase n°5  

Cualquier duda me escriben a vaninamedinasecundaria@gmail.com

CONTINUACIÓN DE LA CLASE 5

ACTIVIDAD 3

Responde planteando la ecuación correspondiente. Luego verifica la solución. Observa el ejercicio C que se da como ejemplo.

A)    Al doble de un número le sumé 1 y obtuve 309. ¿Cuál es el número?

B)    A un número le busco su cuádruple y luego le sumo 51, eso da 159. ¿Cuál es el número?

C)    ¿Cuál es la edad de Rodrigo, si dentro de 32 años tendrá el doble de 41?

Ecuación                                 Verificación                           

R + 32 = 2 . 41                       R + 32 = 2 . 41

R  + 32 = 82                          50 + 32 = 2 . 41

R          = 82 – 32                       82     =  82

R          = 50

Vemos entonces que Rodrigo tiene 50 años

D)    A la mitad de un número se le resta 1 y se obtiene la tercera parte de 213. ¿De qué número se trata?

ACTIVIDAD 4

Martin cometió algunos errores al resolver ecuaciones. Nombra cuáles son y resuelve correctamente.

A)    3x + 21 = 171                         B) 7x – 13.4 = 200

   x + 21 = 171:3                          7x – 13 = 200:4

        x    = 57 – 21                              7x   = 50 + 13

            x = 36                                      x = 63:7

                                                                         x = 9

Una opción para saber que las respuestas son incorrectas es realizar la verificación, pues encontrarán que los resultados de ambos miembros no darán una igualdad verdadera.

ACTIVIDAD 5

Encuentren el valor de cada incógnita y verifiquen

A)              8 + m = 5²

B)              T – 8 = 2³

C)              y³ = 2⁵.2

D)      RAÍZ CUADRADA DE N    = 3² + 5⁰

Aclaración: En esta última actividad la letra x se ha reemplazado por otras, ya que la incógnita puede ser representada por cualquier letra del abecedario.

MATEMÁTICA 

FECHA: 06/07/2020

CLASE: 7

TEMA: ECUACIONES DESPEJE DE INCOGNITA 

Hola 1° F  les adjunto la clase n° 7 correspondiente a la clave de corrección de la clase 5 y 6

Cualquier duda me escriben a vaninamedinasecundaria@gmail.com

CLAVE DE CORRECCIÓN. ECUACIONES. PARTE 2 ACTIVIDAD 1 Resuelve, pensando en esta nueva idea de “pasar” los números para despejar a x. 
A) x + 4 = 15
 x = 15 – 4 
x = 11 
B) x – 12 = 19
 x = 19 + 12
 x = 31 
C) x . 4 = 16
 x = 16 : 4 
x = 4 
D) x : 6 = 5 
x = 5.6 
x = 30

---------------------------------------------------------

1° F    EDUCACION ARTISTICA (PLASTICA)


HOLA CHICOS ,ESPERO QUE SE ENCUENTREN BIEN  JUNTO A SU FAMILA.
HAY NUEVA ACTIVIDAD PERO , A PARTIR DE HOY DESDE EL CLASSROOM.
DEBEN MARCAR LAS TAREAS COMO COMPLETADAS , LAS QUE YA FUERON ENTREGADAS. 
LES DEJO EL CODIGO:    ( tprrjyw)

SALUDOS CUIDENSE MUCHO
-------------------------------------------------------------